https://www.acmicpc.net/problem/3199
3199번: ABCD
정찰 부대가 지금 막 새로운 보고를 보내왔습니다. 그 보고의 내용은 바로, ABCD(Atomic Beryllium-Cesium Destroyer)라는, 이름만 들어도 소름이 끼치는 병기가 테러리스트들에게 넘어갔다는 것입니다. ABCD
www.acmicpc.net
부품들이 4개의 레일 위를 이동하면서 정확히 직사각형을 만들 때 자폭한다. 폭발력은 직사각형의 넓이다. 최소한 넓이를 줄여야 한다.
기하학다운 문제다. 풀리니 짜릿하다!
접근
직사각형의 성질중에 마주보는 변의 길이가 같다는 점을 생각했다. 만약 A와 B의 길이가 C와 D의 길이와 다르다면 마주보는 변의 길이가 같을까?

정확하게 그리지 못했지만 아무튼 직사각형의 꼭짓점이 올바르게 있지 않다. 즉, A-B의 길이가 C-D의 길이와 같지 않다면 자폭에 실패한다는 말이다.
자폭에 실패하는 경우는 구했는데, 자폭에 성공했을 때 피해를 최소화하기 위해 최소 넓이를 구해야 한다.
이 문제는 고등학교 수업을 잘 들었다면 충분히 풀 수 있다. 최소 넓이를 구하는 함수가 있다고 하면 그 함수의 도함수가 0이 되는 위치를 찾으면 된다.
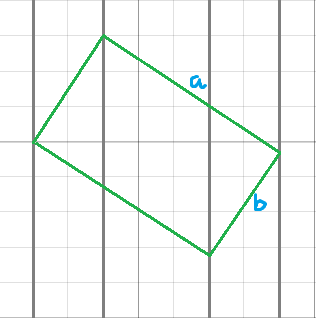
위 사진 처럼 임의의 직사각형을 구성하고 밑변과 높이의 값을 a,b라고 두었을 때 직사각형의 넓이는 S=a*b이다.
a와 b의 길이를 구하기 위해 선분 b와 레일 A사이의 각도를 θ라고 두면, a와 b는 이렇게 표현할 수 있다.
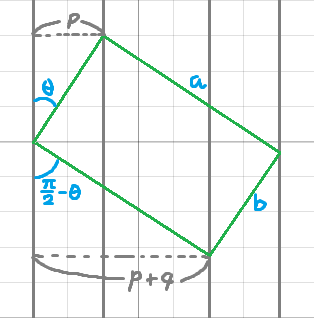
$$ sin({{\pi\over 2} - \theta}) = cos\theta = {{p+q}\over a},\\ \therefore a = {{p+q}\over {cos\theta}} $$
$$ sin\theta = {p\over b},\\ \therefore b = {p\over sin\theta} $$
위 식을 조합하면 넓이를 나타내는 함수는 다음과 같다.
$$ S(\theta) = p(p+q) \times {1\over sin\theta } \times {1\over cos\theta} $$
이 함수의 도함수가 0이 되는 부분이 있다면 함수의 최대 또는 최소를 의미할 것이다.
p(p+q)부분은 상수이므로 사라지고 뒷부분만 남게된다. 미분을 하면 다음처럼 정리된다.
$$ S'(\theta) = ({1\over sin\theta} \times {1\over cos\theta})' \\ = {1\over{\sqrt{1-\theta^2}}}{1\over cos\theta} - {1\over{\sqrt{1-\theta^2}}}{1\over sin\theta} \\ = {1\over{\sqrt{1-\theta^2}}}({1\over cos\theta} - {1\over sin\theta}) \\ \therefore S'(\theta) = {1\over{\sqrt{1-\theta^2}}}{(sin\theta - cos\theta)} $$
//[ {1\over \sqrt{1-\theta^2}} ]// 에서는 도함수가 0이 될만한 값을 찾을 수 없고, //[ (sin\theta - cos\theta) ]// 에서 찾을 수 있다.
//[ sin\theta = cos\theta, \therefore \theta = {\pi\over 4} ]// 이고, //[\theta = {\pi\over 4}]//에서 부호를 비교해보면,

음에서 양으로 가는 모습이 보인다. 최소다!
이제 직사각형의 밑변과 A레일간의 각도가 45도라면 최소 넓이를 구할 수 있음을 알아냈다.
θ값을 각 식에 대입하면,
$$ a = {{p+q}\over cos{\pi\over 4}} = \sqrt2 \times (p+q), \\ b = {p\over sin{\pi\over 4}} = \sqrt2 \times p, \\ \therefore S(\theta) = 2 \times p \times (p+q) $$
결과를 얻기까지 많은 시간이 들었는데 너무 짧은 공식으로 정리되어 허무한 느낌이 든다.
미흡했던 점
처음엔 직사각형의 각 대각선 길이에 뭔가 있지 않을까 해서 식을 세우려고 해봤는데 너무 복잡해졌다. 이런 접근도 나쁘지 않았다. 각도를 이용해 풀어보는 생각을 했기 때문이다.
미분공식을 까먹어서 검색을 했다는게 조금 부끄럽다.
#include <iostream>
int main() {
double p, q, r;
scanf("%lf %lf %lf", &p, &q, &r);
if (p != r) {
printf("0");
return 0;
}
printf("%.4lf", p * (p + q) * 2);
}
댓글