멀티코어프로그래밍 (3) - [논문 리뷰] Extending Amdahl’s Law for Energy-Efficient Computing in the Many-Core Era
2024년 2학기 멀티코어프로그래밍 수업을 듣고 정리한 내용입니다. 수업 교재는 Computer Architecture: A Quantitative Approach입니다.
멀티코어프로그래밍 과목에서 내가 했었던 논문 리뷰 발표다. 본 수업은 학생마다 모두 논문 1개를 읽고 발표하는 활동이 진행되었다. 나는 Extending Amdahl’s Law for Energy-Efficient Computing in the Many-Core Era논문을 선택해 발표를 했다.

아래는 논문 대본 내용과 발표 슬라이드다.

암달의 법칙은 코어를 많이 넣어도 순차적 작업 때문에 성능 향상이 어려움. 개선을 위해 여러 방법이 연구되었지만 근본적으로 성능 향상을 위해 코어를 많이 넣는다면 전력이 많이 들어가는 문제점이 대두됨.
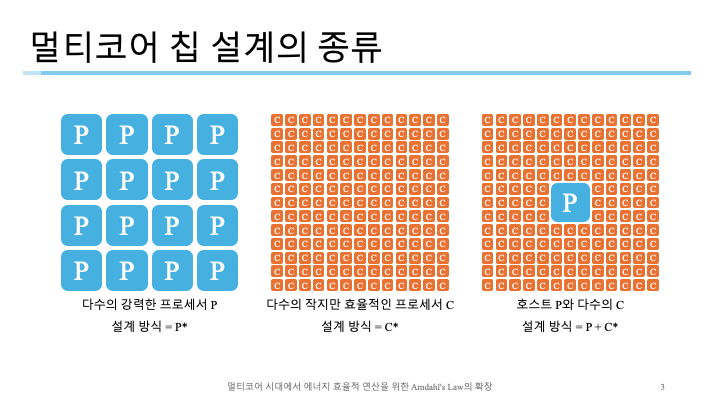
저자는 3가지 모델을 제시함.
- 높은 퍼포먼스를 보이는 P코어가 모인
P* - 퍼포먼스가 낮은 대신 효율이 좋은 C코어가 모인
C* - P 하나와
C*를 결합한P + C*
저자는 각각의 모델마다 암달의 법칙을 확장하여 전력 모델을 제시합니다.

암달의 법칙은 순차적 작업을 처리하는 부분, 병렬적 작업을 처리하는 부분을 분모로 둠. 순차적 작업을 처리할 때 한 개 코어를 제외한 나머지 코어는 유휴상태이고 이 때 $k$만큼 전력을 소모함 ($k$는 비율, 1이면 완전히 활성화된 상태)
W는 평균 전력으로 처리하는 시간을 분모로 하고 소모한 전력량을 분자로 한다. 순차 처리할 때는 한 개의 코어만 1로 동작, 나머지는 $k$로 동작하므로 정리하면 다음과 같다.
$\frac{Perf}{W}$는 전력대성능비 줄여서 전성비라고 하고 $W$를 뒤집어서 곱하면 됨. 정리하면 이렇게 된다.
$J$는 에너지의 단위로 $\frac{Perf}{J}$는 에너지대성능비라고 할 수 있고, 이 논문에선 에너지효율로 이해할 수 있음.

P와 비교하기 위해 P와 C의 성능 차이를 $s_c$로 정규화시켜 표현. 성능 차이와 비슷하게 전력 소모율도 $w_c$로 정규화시켜 표현.
성능과 전력이 정규화되어 표현된 모습
전성비와 에너지효율을 전개한 모습...
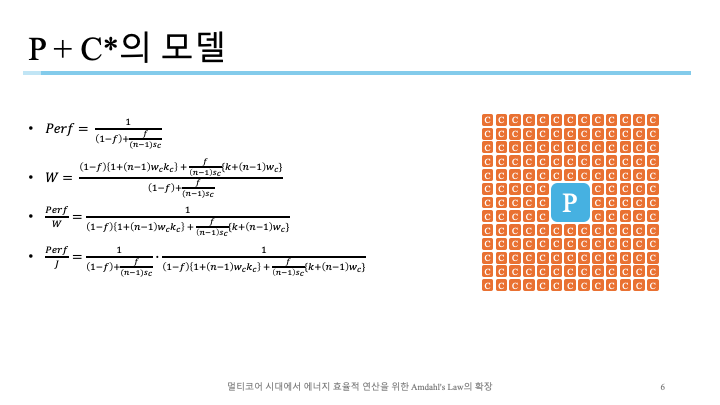
순차적 처리는 P가 담당하고 병렬적 처리는 C*가 담당하는 모습으로, $1-f$에는 P가 $\frac{f}{n}$은 C*가 담당하여 성능이 표현됨
전력식이 조금 복잡한데, $1-f$는 순차적 처리이므로 P는 $k=1$, C*는 $w_c\times k_c$ 즉 정규화값과 유휴상태의 전력소모율가 곱해진 모습. $\frac{f}{(n-1)s_c}$는 병렬적 처리이므로 P는 $k$, C*는 $w_c$가 곱해진 모습.
전개하면 전성비와 에너지효율식을 얻을 수 있다.
저자는 앞서 간단하게 살펴본 식들을 그래프를 통하여 분석했습니다.
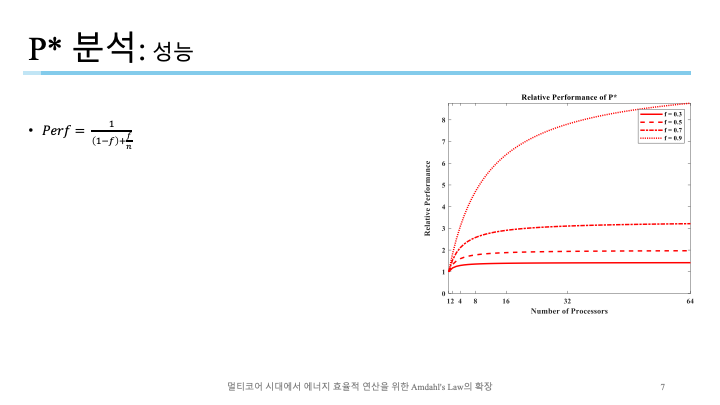
논문에서 제시한 그래프를 그대로 쓸 수도 있지만 발표에서 사용할 이미지는 항상 깔끔하고 부드러워 보여야 한다고 생각해 직접 매트랩 코드를 작성했습니다.
코어 수가 많아질수록 성능이 늘어나지만 한계가 있음이 보임.
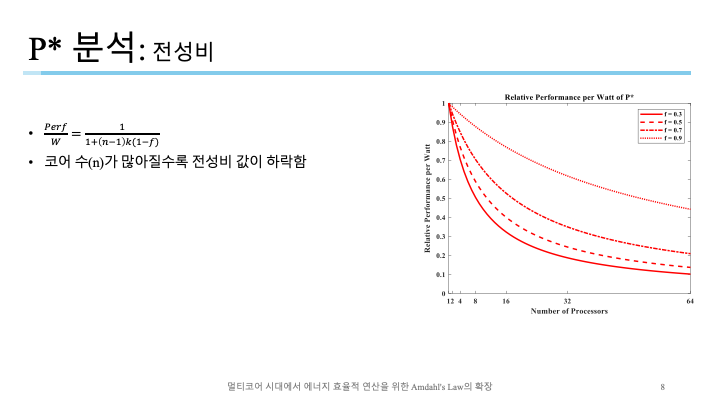
코어가 하나라면 전성비 값이 $1$로, 전력을 소모한 만큼 일의 효율을 보임. 전성비가 $1$보다 높으면 아웃풋이 좋다고 생각할 수 있음.
그러나 P모델은 코어가 많아지면 전성비가 하락함. 이 부분은 병렬화비율을 높여서 줄여볼 수 있지만 무조건 $1$보다 낮아지게 됨.
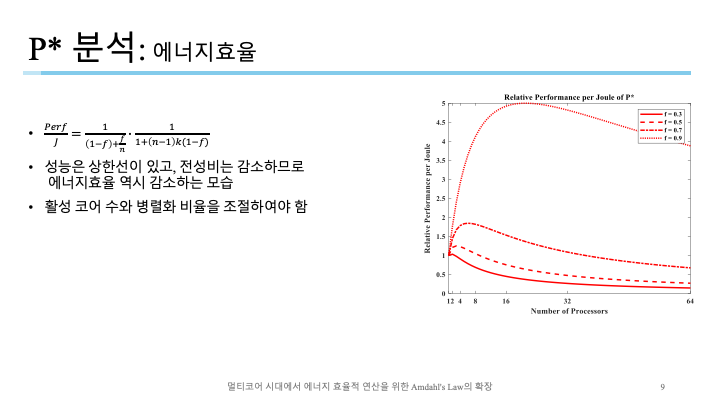
간단하게 보자면 성능은 한계점을 가지고, 전성비는 $1$보다 낮고 감소하기 때문에 전체적으로 감소하는 모습.
그러나 최대값을 갖기 때문에 코어를 다수 보유하고 있다면 병렬화 비율과 활성 코어수를 런타임에 조절하여 에너지효율을 최대로 만들 수 있음.
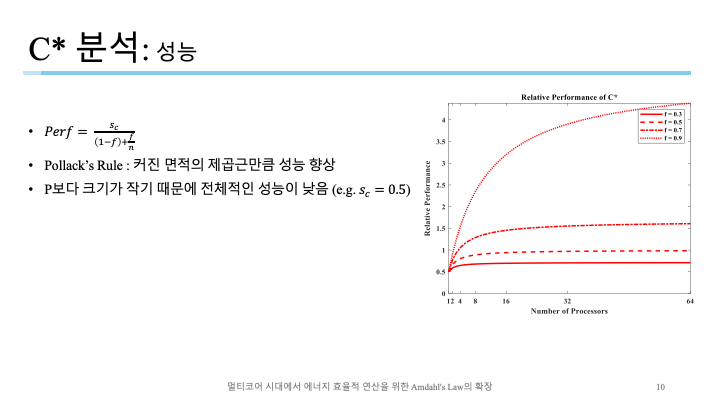
정규화하여 표현한 모습, P보다 성능이 낮은데 당연하게도 크기가 작은 C는 성능이 낮다고 생각할수 있음. 저자는 $s_c$를 $0.5$로 설정하고 추정했음
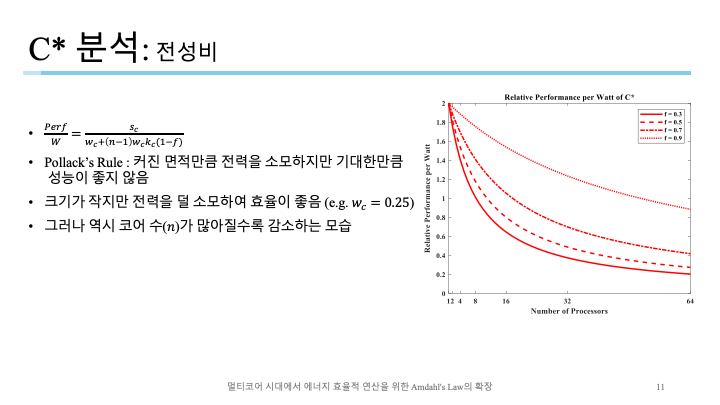
폴락의 법칙은 칩의 면적이 커지면 커진 면적의 제곱근만큼 성능이 나온다는 것인데 다시 생각하면 커진 면적만큼 전력이 공급되지만 기대한만큼 성능을 얻지 못한다는 뜻. 즉 C보다 P가 크기가 더 크기 때문에 P의 전성비가 좋지 않다는 말임. 저자는 $w_c$를 $0.25$로 설정했는데 그래프에서 C는 전성비가 $2$에서 시작하는 모습을 볼 수 있음 그러나 코어 수가 많아질수록 역시 전성비가 하락하는 모습.
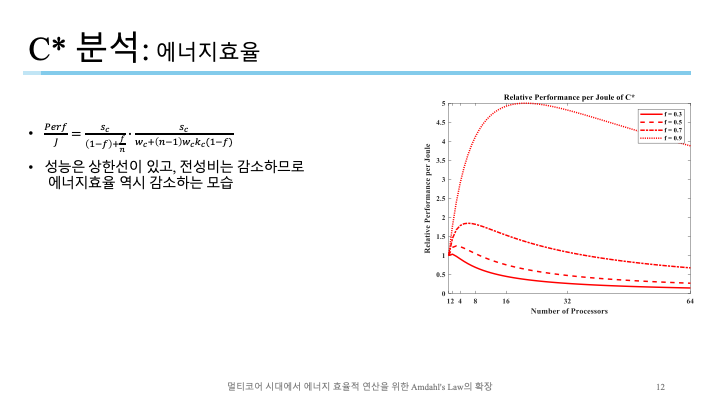
P와 유사한 기조로 에너지효율을 보이는 모습.
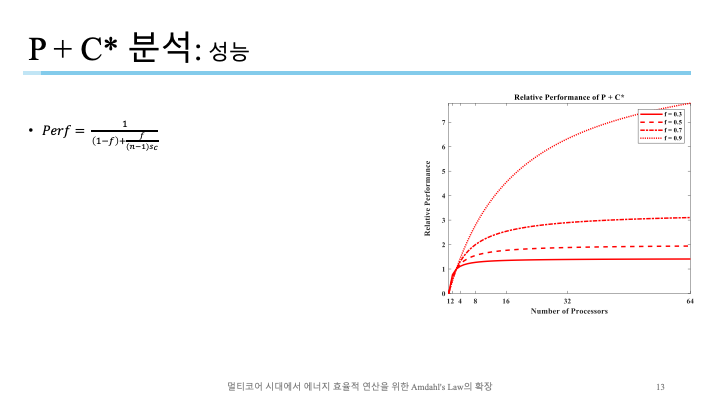
성능은 P와 비슷하지만 약간 못미치는 수준.
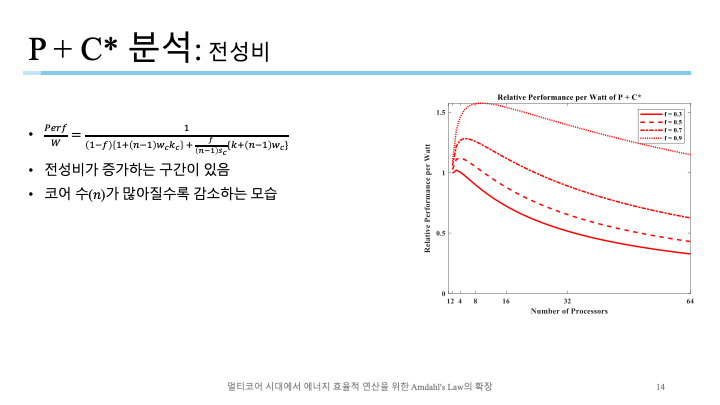
전성비가 $1$에서 시작하지만 증가하는 구간이 있음. 코어 수가 적을 때 C가 추가됨으로 더해지는 전력량보다 성능이 더 좋은 시기임(전성비가 $1$ 이상이니까). 그러나 코어수가 많아지면 전성비가 $1$ 이하로 내려가니까 전체적인 전성비가 하락함.
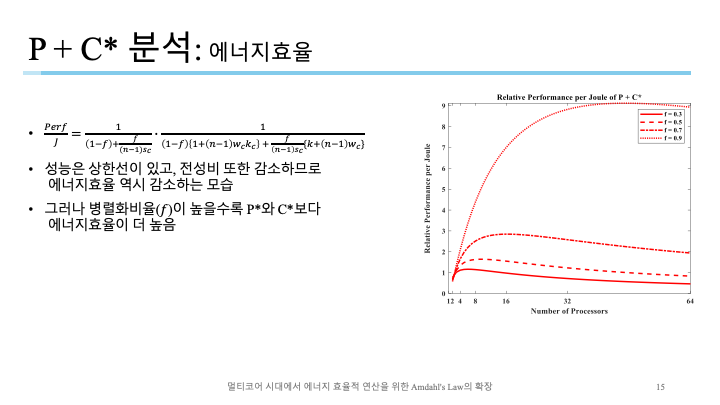
다른 모델과 동일하게 전체적으로 코어수가 많아질수록 에너지효율이 감소하지만 P*나 C*보다 에너지 효율이 좋은 모습.
순차 실행과 병렬적 실행을 동시에 하기 때문에 비교적 처리를 잘한다고 볼 수 있음.

논문에서는 설계방식을 소개한 후 전력예산에 대해 소개했는데 이해를 위해 여기서 발표함.
서론에서 제시했듯이 코어를 많이 넣으면 전력이 많이 들어감. 따라서 전력을 제한한 상태에서 설계가 진행되어야 함.
P*가 활성상태일 때 전력소모비율이 $1$이므로 P의 코어 수는 $N_p$
C*는 P의 전력소모비율을 정규화시키면 되므로 코어 수는 $\frac{W_{budget}}{w_c}$이 됨
P + C*는 P $1$개에 나머지 C이므로 $1 + \frac{W_{budget}-1}{w_c}$
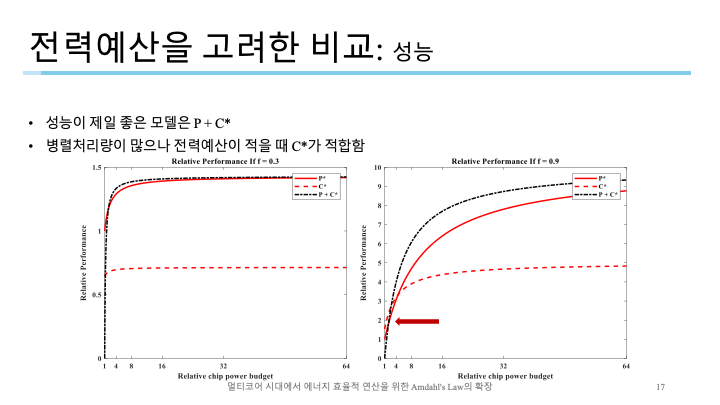
앞서 전력예산을 제한시킨 상태에서 가능한 최대코어의 수를 계산했으므로 전력예산의 값을 조절하면서 성능, 전성비, 에너지효율을 추정해볼 수 있음.
왼쪽은 $f=0.3$, 오른쪽은 $f=0.9$인데 전체적으로 P + C*가 가장 높은 성능을 보임
C는 성능이 좋지 않지만 병렬화비율이 높고 전력예산이 낮을 때 가장 좋음(화살표가 가리키는 부분에서 C*의 성능이 가장 좋음)
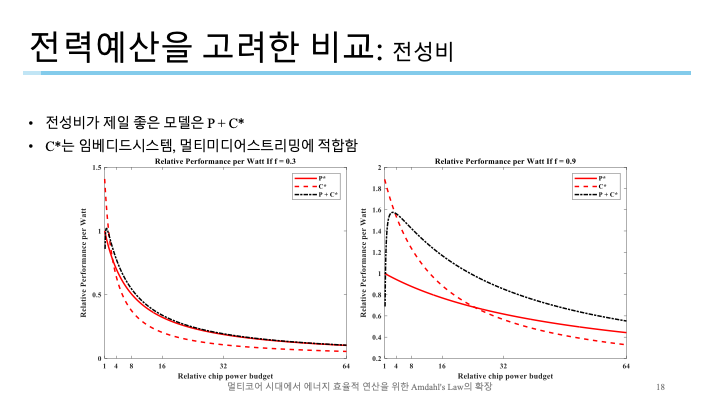
전력예산이 적당할 때에는 P + C*가 좋지만 매우 적은 전력예산을 가진 상황에서는 C*가 가장 좋음. 따라서 임베디드 또는 멀티미디어 스트림같은 환경에 적합한 모델임
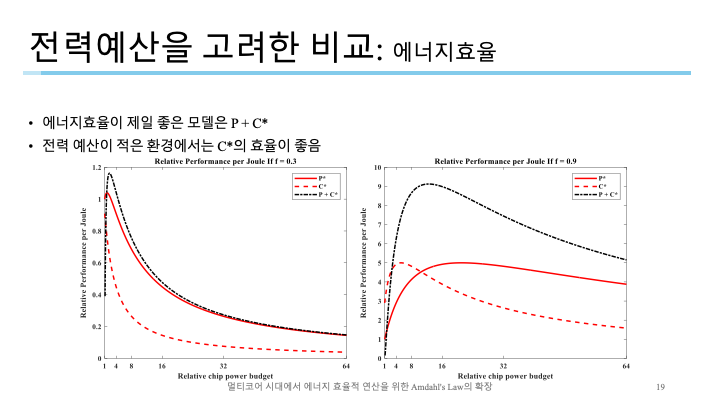
P + C*가 가장 좋고, 여기서도 C*는 전력예산이 적을때 좋은 모습

논문에서는 다른 변수($k_c$, $s_c$ 등)들을 다르게 설정하여 추정했지만 그래프와 유사하게 나타났다고 함.