운영체제 (9) - Uniprocessor Scheduling
2024년 1학기 운영체제 수업을 듣고 정리한 내용입니다. 수업 교재는 운영체제 - 내부구조 및 설계원리 8 판입니다.
Aim of Scheduling
프로세서가 한 개인 시스템에서 여러 프로세스를 스케줄링할 때 다음과 같은 목표를 달성하는 방향으로 전략을 짠다.
- 응답 시간
- Throughput (단위 시간동안 실행을 완료한 프로세스 수)
- Processor efficiency (CPU 사용도, OS보다 유저 프로그램을 많이 실행하면 좋은 것)
- Fiarness (모든 프로세스에게 공정한 실행 기회)
그러나 모든 목표를 신경쓰면서 할 수 없기 때문에 이 중에 한 가지만이라도 집중하는 방향으로 전략을 짜게 된다.
수업시간에는 응답 시간에 집중하는 방향으로 배운 것 같다.
Type of Scheduling
프로세스 스케줄링이 일어나는 위치는 세 곳이다.
- Long-term (프로세스 생성 시)
- Medium-term (프로세스 Swapping)
- Short-term (다음에 실행할 프로세스 선택)
Long-term과 Medium-term은 성능 개선이 어렵지만 Short-term과 같이 다음에 실행할 프로세스를 잘 선택하면 전체 실행 시간이 결정된다.
Short-Term Scheduling Criteria
사용자 측면에서는 입력한 요청이 빠르게 처리되어야 하므로 아래의 두 가지 측면에서 성능을 판단한다.
- Response Time (입력 후 출력까지 걸린 시간)
- Turnaround Time (실행 후 종료까지 걸린 시간)
OS 측면에서는 불필요한 스위칭이나 OS작업을 하지 않고 유저 프로그램을 많이 돌려야 성능이 좋다고 여겨진다.
성능 외적으로는 내 프로세스가 언제 끝날지 알 수 있는 것을 의미하는 예측 가능성과 같은 기준을 적용받는 프로세스들 사이에 공평한 실행 기회를 받는 공정성으로 판단할 수 있다.
Priorities
모든 프로세스는 우선순위값을 가지고, 이 우선순위값에 의해 스케줄링된다.

예시를 들기 위해 위의 사진처럼 5개의 프로세스가 도착한 시간과 각각 작업에 걸리는 시간을 가정한다.
First-Come-First-Served
- 먼저 도착한 프로세스부터 처리한다. 들어온 순위가 곧 우선순위이다.
- Non-preemption이다. (일단 시작하면 끝날때까지 프로세스를 바꾸지 않는다.)

파란색 부분은 실행시간, 투명한 회색 부분은 대기시간이다.
$$
A = 0 + 3 = 3\newline
B = 1 + 5 = 6\newline
C = 5 + 4 = 9\newline
D = 5 + 5 = 10\newline
E = 6 + 4 = 10\newline
평균 실행 시간 = \frac{3+6+9+10+10}{5} = \frac{38}{5} = 7.6
$$
Round-Robin
- 정해진 Quantom동안 프로세스를 실행한 후 교체한다. 교체할 프로세스는 Ready 큐에서 꺼내고, Timeout된 프로세스는 다시 큐에 넣는다.
- Preemption이다.
여기서는 Q = 1로 가정하고 예시를 들어보면 아래 사진처럼 나타난다.

먼저 0초부터 2초까지는 프로세스 A만 존재하므로 그대로 실행한다. 하지만 2초에 B가 등장한다. 여기서 새로 등장하는 프로세스가 현재 실행을 마친 프로세스보다 먼저 처리된다고 가정하고 실행되었다. OS마다 다르게 처리할 수 있지만 일단 예시를 들기위해 그렇게 처리했다.
3초에 C가 등장하지만 현재 B가 실행되고 있을 때 큐의 상태는 [A]이다. 새로 들어오는 프로세스가 현재 실행을 마치고 다시 큐로 들어가려는 프로세스보다 먼저 큐에 들어간다는 가정을 했었기 때문에 B 다음엔 A가 실행되고 큐에는 [C, B]가 들어있게 된다. 4초에는 바로 C가 실행된 모습이다.
$$
A = 1 + 3 = 4\newline
B = 9 + 5 = 14\newline
C = 6 + 4 = 10\newline
D = 7 + 5 = 12\newline
E = 3 + 4 = 7\newline
평균 실행 시간 = \frac{4+14+10+12+7}{5} = \frac{47}{5} = 9.4
$$
Shortest Process Next
- 실행 가능한 프로세스중 가장 작업에 걸리는 시간이 짧은 프로세스부터 실행한다.
- Non-preemption이다.
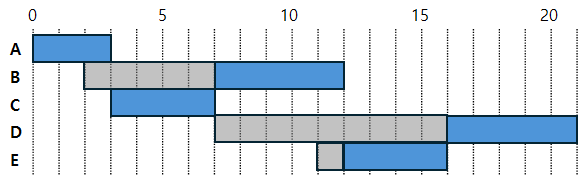
0초에는 A밖에 없기 때문에 A를 끝까지 실행한다.
3초에 A가 종료되면 B와 C가 도착하였는데, C가 더 작업시간이 짧으므로 C부터 실행한다. C가 실행을 마치면 7초가 된다.
7초에는 D가 도착해서 B와 D가 후보로 있는 상태인데, 둘 다 작업시간이 같으므로 먼저 도착한 B부터 실행한다.
B가 실행을 마친 12초에는 E가 도착해서 D와 E가 후보로 있다. E가 더 작업시간이 짧으므로 E를 실행한 다음 D를 실행한다.
$$
A = 0+3 = 3\newline
B = 5+5 = 10\newline
C = 0+4 = 4\newline
D = 9+5 = 14\newline
E = 1+4 = 5\newline
평균 실행 시간 = \frac{3+10+4+14+5}{5} = \frac{36}{5} = 7.2
$$
Prediction of execution time
하지만, 실제로 어떤 프로세스가 제일 짧은 실행 시간을 갖는지 정확하게 알 방법은 없다. 그래서 예측된 실행시간을 사용해야한다.
산술적으로 예측한다면 총 실행 시간을 실행 횟수로 나눠 예측할 수 있다.
$$
S_{n+1} = \frac{1}{n}\sum_{i=1}^{n}{T_i}
$$
n번까지의 실행 시간($T_n)을 합한 값을 n으로 나눠서 다음 번의 실행 시간을 예측한다.
기하적으로 예측한다면 이전 실행 시간과 이전에 예측한 값에 각각 가중치를 부여하여 다음 실행 시간을 예측한다.
$$
S_{n+1} = {\alpha}T_n+(1-\alpha)S_n
$$
두 가지 방법을 적용하여 통계를 낸 결과는 다음과 같다.

Simple average 그래프는 산술적 방법을 적용한 결과이고, $\alpha$가 있는 그래프는 기하적 방법을 적용한 결과이다. Observed value 그래프는 실제 실행 시간을 나타낸 것인데, 실제 실행 시간이 늘어나면 늘어날 수록 산술적 방법보다 기하적 방법이 오차가 적음을 알 수 있다.
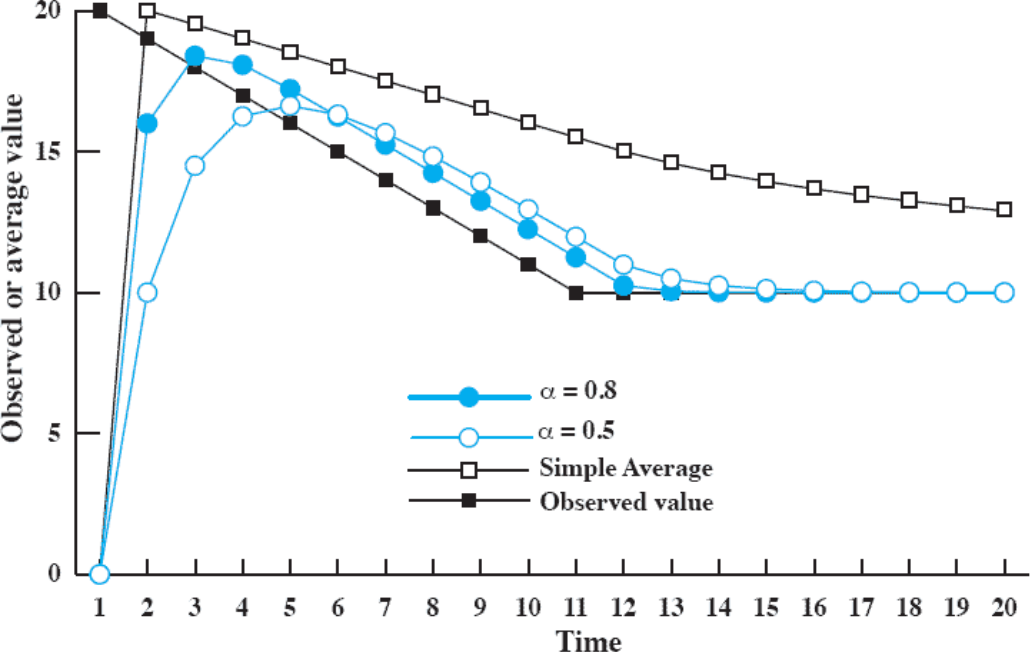
반대로 실행 시간을 점점 줄여볼 때 초기에는 산술적 방법이 오차가 적지만 점점 기하적 방법이 오차가 적음을 알 수 있다.
Shortest Remaining Time
- 프로세스를 실행하되 종료까지 남은 시간이 제일 짧은 프로세스를 실행한다.
- Preemption이다.

0초에 A가 도착하여 A가 실행된다. 2초에 B가 도착하지만 A는 종료까지 남은 시간이 1초이고 B는 5초다. 따라서 A가 실행된다.
3초에 C가 도착하게 되는데 B와 C중에 C가 4초로 더 짧다. 따라서 C가 실행된다.
7초에 D가 도착하지만 B와 D는 모두 실행시간이 같으므로 먼저 도착한 B가 실행된다.
11초에 E가 도착하지만 B는 1초, D는 5초, E는 4초로 B가 제일 짧기 때문에 계속 실행된다.
B가 실행을 마친 12초에는 D와 E중에 E가 더 짧으므로 E가 실행을 하게 되고 최종적으로 D가 실행을 하게 된다.
예시에서는 Non-preemption처럼 보이는데, 프로세스가 실행중에 종료까지 남은 시간이 더 짧은 프로세스가 등장한다면 그 프로세스로 바꾸어 실행한다.
$$
A = 0+3=3\newline
B = 5+5=10\newline
C = 0+4=4\newline
D = 9+5=14\newline
E = 1+4=5\newline
평균 실행 시간 = \frac{3+10+4+14+5}{5} = \frac{36}{5}=7.2
$$
Highest Response Ratio Next
- 다음 공식에 따라 우선순위를 정하고 우선순위가 더 높은 프로세스부터 실행한다.
$$
우선순위 = 1 + \frac{기다린 시간}{예상 실행 시간}
$$ - Non-preemption이다.

Starvation을 해결하기 위해 등장한 방법이다. 우선순위를 정하는 방법에 기다린 시간을 분자로, 예상 실행 시간을 분모로 설정한다. 예상 실행 시간이 짧거나, 기다린 시간이 길어질수록 값이 커진다. 만약 기다린 시간이 같다면 예상 실행 시간이 짧은 프로세스부터 실행된다. 반대로 예상 실행 시간이 같다면 기다린 시간이 긴 프로세스부터 실행된다.
A가 실행을 마친 3초에는 B와 C가 후보로 존재한다. B는 $1+\frac{1}{5}=1.2$이고 C는 $1+\frac{0}{4}=1$이다. 따라서 B가 값이 더 크기 때문에 B를 실행한다.
B가 실행을 마친 8초에는 C와 D가 후보로 존재한다. C는 $1+\frac{5}{4}=2.25$이고 D는 $1+\frac{1}{5}$이다. C가 값이 더 높으므로 C를 실행한다.
C가 실행을 마친 12초에는 E가 도착하여 D와 E가 후보로 존재한다. D는 $1+\frac{5}{5}=2$이고 E는 $1+\frac{1}{4}=1.25$이다. E가 실행 시간이 더 짧지만 D가 오래 기다려서 우선순위값이 높아졌으므로 D를 실행한다.
$$
A=0+3=3\newline
B=1+5=6\newline
C=5+4=9\newline
D=5+5=10\newline
E=6+4=10\newline
평균 실행 시간 = \frac{3+6+9+10+10}{5}=\frac{38}{5}=7.6
$$
비교
전체적으로 실행 시간을 비교해보면,
FCFS = 7.6
Round-Robin = 9.4
SPN = 7.2
SRT = 7.2
HRRN = 7.6
SPN과 SRT가 평균적으로 실행을 제일 먼저 끝내고, FCFS와 HRRN이 그 다음으로 실행 시간이 빠르다. Round-Robin은 끔찍한 실행 시간을 보여준다.
통계적으로는 SPN과 SRT가 가장 빠르고 FCFS와 Round-Robin이 가장 느린 반면 HRRN은 그 사이에 위치해 있다고 한다.
Feedback
그런데, 실행 시간을 정확하게 알지 못하기 때문에 매 순간 예측을 해야한다는 단점을 갖는다. 실행시간을 예측하기 위해 연산하는 것은 굉장히 큰 비용이 들기 때문에 위에서 본 방법들을 전부 사용할 수 없다.
실행 시간이 짧은 프로세스를 찾기보다, 실행 시간이 긴 프로세스를 찾는 게 훨씬 간단하다. 당연하게도 여러 프로세스들을 실행하면서 실행이 끝나지 않는 프로세스가 실행 시간이 긴 프로세스일 것이다.
Feedback 방식은 여러 큐에 우선순위를 부여해서 우선순위가 높은 큐부터 실행하고, 정해진 시간만큼 실행을 마친 프로세스를 더 낮은 우선순위의 큐로 보내는 방식이다. 즉, 낮은 우선순위의 큐에 있는 프로세스는 실행 시간이 긴 프로세스임이 확실한 것이다.
낮은 우선순위를 가진 프로세스는 분명히 긴 시간동안 실행해야 종료될 것이므로 높은 우선순위를 가진 프로세스와 같은 시간 실행하면 당연히 오래 걸리게 될 것이다. 그러므로 낮은 우선순위의 프로세스들은 긴 실행시간을 갖도록 설정하여 기회를 잡았을 때 최대한 길게 실행하도록 한다. 여기서는 우선순위가 p일 때 $2^{p}$의 실행시간을 갖도록 설정했다.

먼저 0초에 A가 등장한다. 2초 후에 B가 등장하니까 그 전까지 A가 실행된다. 하지만 우선순위가 바뀌지 않고 계속 0에 남아있는데, 굳이 우선순위를 이동시킬 필요가 없기 때문이다. (어차피 후보가 A뿐이므로)

2초에는 B가 등장한다. 0번에 있기 때문에 직전에 실행했던 A는 우선순위가 한 단계 낮아져 1로 간다. 그리고 B는 $2^0$시간만큼 실행된다.
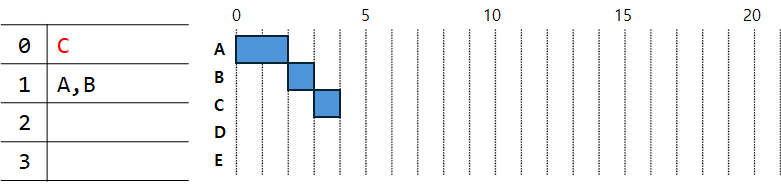
3초에 C가 등장하므로 B는 1번 큐로 이동하고, C가 $2^0$시간만큼 실행된다.

4초에는 0번 큐가 비었기 때문에 A가 실행된다. $2^1$시간만큼 실행되어야 하지만, A는 3초동안 실행을 할 경우 종료되기 때문에 1초만 실행하게 된다.

5초에는 B가 실행된다. $2^1$시간만큼 실행된다. 실행을 마치면 2번 큐로 이동한다.

7초에는 D가 등장하므로, D가 1초만큼 실행된다. 실행을 마치면 1번 큐로 이동한다.

8초에는 0번 큐가 비어 1번 큐를 확인하게 되고 C가 실행된다. C는 $2^1$시간만큼 실행되고 2번 큐로 이동한다.

10초에는 1번 큐에 있는 D가 실행된다. D는 $2^1$시간만큼 실행되어야 하지만, 11초에 E가 등장한다. 10초에는 D가 실행되고 11초에는 더 높은 우선순위를 가진 E가 실행된다. D는 실행중에 우선순위가 더 높은 프로세스에게 실행을 뺏겨버렸으므로 다시 1번 큐로 진입하게 된다.

12초에는 1번 큐에 있는 D가 실행된다. 실행을 마치면 2번 큐로 이동한다.

14초에는 1번 큐에 남아있는 E가 실행된다. 실행을 마치면 2번 큐로 이동한다.
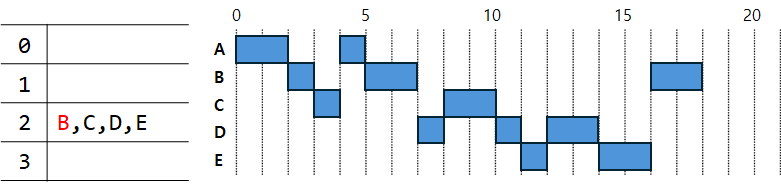
16초에는 B가 실행된다. 이 때에는 $2^2$시간만큼 실행되어야 하지만 B는 2초만 수행하면 프로세스를 종료할 수 있으므로 2초만 실행하고 사라지게 된다.
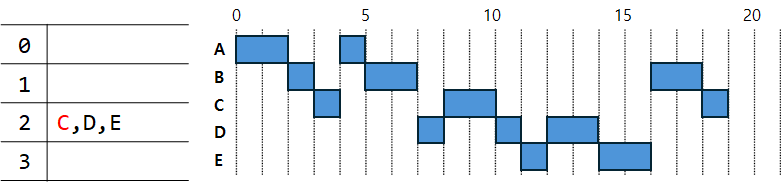
18초에는 C가 실행되는데 C 또한 1초만 실행하면 종료된다.

19초에는 D가 실행되는데 D 역시 1초 후 종료된다.

마지막으로 E가 1초동안 실행한 뒤 종료되면서 모든 프로세스가 종료된다.
Fair-Share Scheduling
한 프로그램이 한 프로세스안에서 실행되면 다른 프로세스들과 공평하게 실행이 되지만, 여러 프로세스에 나뉘어 실행된다면 다른 프로세스보다 CPU를 더 많이 차지하는 꼼수가 있다. 따라서 Fair-Share 방식은 프로세스 단위가 아닌 어플리케이션 단위로 실행한다.
Traditional UNIX Scheduling
UNIX는 Multilevel feedback using Round-Robin 방식을 사용한다. 앞서 보았던 Feedback 방식을 사용하되, 같은 큐에 있는 프로세스들을 Round-Robin 방식으로 실행하는 것이다. Round-Robin 방식으로 실행할 때에는 Timeout되어도 다른 큐로 이동하지 않는다. 그리고 프로세스가 모두 Blocked되면 그 때 다음 큐에 있는 프로세스를 실행한다.
특별한 점은 모든 프로세스의 우선순위를 1초마다 다시 계산한다는 것이다. 우선순위를 다시 계산한다는 것은 곧 큐에 있는 프로세스가 이동한다는 말이다. 프로세스의 우선순위는 프로세스의 타입과 실행 시간 등으로 계산한다.
프로세스 $j$의 우선순위$P_j$는 다음 공식에 의해 계산된다.
$$
CPU_j(i) = \frac{CPU_j(i-1)}{2}\newline
P_j(i) = Base_j + \frac{CPU_j(i)}{2} + nice_j
$$
$CPU_j(i)$는 $i$초에서 프로세스 $j$의 CPU 사용도다.
$Base_j$는 프로세스 $j$의 기본 우선순위다.
$nice_j$는 사용자가 정한 프로세스 $j$의 우선순위다.
$P_j$는 프로세스 $j$의 우선순위로 값이 낮을 수록 우선순위가 높다.
$CPU_j(i)$를 구하려면 $CPU_j(i-1)$의 값에 2를 나누면 된다. 예를 들어 1초에 CPU를 0.5만큼 사용했다면, 2초에 $CPU_j$값은 $\frac{0.5}{2}=0.25$다. 이 공식은 이전에 CPU를 사용한 값에 계속 2를 나누므로 CPU를 사용한 기록이 모두 담겨있다. 즉, 1초에 0.5초, 2초에 1초, 3초에 0.25초를 사용했다면 $CPU_j(4)$는 $\frac{0.25}{2} + \frac{1}{4} + \frac{0.5}{8}$이 된다.
$CPU_j$값이 낮다면 우선순위가 높아지게 되는데 CPU를 자주 사용하지 않았다는 뜻이다. 반대로 $CPU_j$값이 높으면 우선순위가 낮아지게 되는데, CPU를 자주 사용했으므로 값이 커지게 된 것이다. 여기서 살펴볼 수 있는 점은 UNIX는 우선순위값을 계속 계산함으로 CPU를 자주 선점하지 못했던 프로세스에게 기회를 주는, 공정성을 우선으로 하는 운영체제인걸 알 수 있다.