2024년 2학기 멀티코어프로그래밍 수업을 듣고 정리한 내용입니다. 수업 교재는 Computer Architecture: A Quantitative Approach입니다.
병렬성의 대두
과거에는 1개의 CPU에 1개 코어, 1개 스레드만 존재했다. 공정을 개선하여 어떻게 하면 1개의 코어가 더 빠르게 연산을 할 수 있을지 고민하였지만, 어느 순간부터 공정의 한계에 다다르게 되었다.
무어의 법칙에 따라 더 많은 트랜지스터를 넣었으므로 더 높은 성능을 얻어야 했지만 실제로는 그렇지 않았다. 경험적으로 얻어진 폴락의 법칙에 따라, 더 많은 트랜지스터를 넣어 면적이 커졌다면 그에 비례해서 성능이 올라가야하지만 실제로는 커진 면적의 제곱근만큼만 성능이 나왔기 때문에 아무리 트랜지스터를 많이 넣고 집적도를 올려도 싱글 코어로는 성능 향상이 크게 나타나지 않았다. 또한 더 많은 트랜지스터를 넣는다면 전력 소모량이 커지기 때문에 소모 전력량을 고려한다면 성능 개선이 쉽지 않게 되었다.
컴퓨터 구조를 세분화하여 명령어를 여러 단계로 나누어 처리하는 과정을 구현함으로 명령어 수준에서 병렬성을 얻는 시도도 있었지만, 분기 명령어와 같이 성능을 저하시키는 명령어 그리고 명령어 간의 의존성 등으로 인해 한계에 다다랐다.
그리하여, 같은 작업을 1개의 코어가 처리하지 말고, 두 개 이상의 코어가 분담하여 처리한다면 성능이 더 좋아지지 않겠냐는 새로운 아이디어가 등장하여 멀티코어 프로세서가 시장을 지배하게 되었다.
병렬성
병렬성에는 두 가지가 있다.
- 데이터 수준 병렬성(DLP) : 데이터를 다루는 동일한 작업의 병렬적 진행
- 작업 수준 병렬성(TLP) : 데이터를 다루는 서로 다른 작업들을 병렬적으로 진행
Flynn's Taxonomy
컴퓨터 아키텍쳐를 4가지로 분류한 것이다.
| 아키텍쳐 | 설명 |
|---|---|
| SISD | 한 번에 데이터 하나를 명령어 하나로 처리하는 기법 |
| SIMD | 한 번에 데이터 여러 개를 명령어 하나로 처리하는 기법 |
| MISD | 한 번에 데이터 하나를 명령어 여러 개로 처리하는 기법 |
| MIMD | 한 번에 데이터 여러 개를 명령어 여러 개로 처리하는 기법 |
데이터 수준 병렬성을 달성하려면 SIMD가 적합하고, 작업 수준 병렬성을 달성하려면 MIMD가 적합하다.
과거와 현재의 인식 차이
| 과거 | 현재 |
|---|---|
| 전력은 제한이 없는 대신 트랜지스터 수가 제한이 될 것 | 전력은 제한이 있는 대신 트랜지스터는 제한이 없을 것 |
| 명령어 레벨에서 병렬화가 충분히 가능할 것 | 명령어 레벨에서 병렬화는 한계에 도달함 |
| 연산은 느리고, 메모리 엑세스가 빠름 | 연산은 빠른데 메모리 엑세스가 느림 |
| 무어의 법칙에 따라 1.5년마다 성능이 2배일 것 | 전력, 명령어레벨, 메모리 엑세스 등에 의해 성능 향상에 한계가 있음 |
big.LITTLE
인텔이 싱글 코어로 성능 향상에 한계를 느끼고 멀티 코어를 도입한 후, 효율적인 전력 활용을 위해 도입한 아키텍쳐다. 강력한 성능을 가진 프로세서(big)와 비교적 작지만 효율적인 전성비를 갖는 프로세서(LITTLE)가 한 칩에 모이는 구조다. 무거운 작업은 big프로세서에게, 가벼운 작업은 LITTLE프로세서에게 맡긴다.
메모리 구조
중앙 집중화 메모리 (Uniform Memory Access)
여러 코어들이 캐시를 갖되 데이터는 한 곳에만 있는 방식
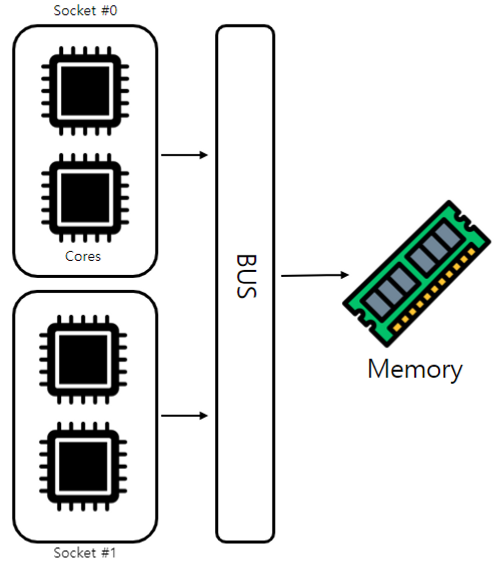
데이터를 가져오기 위해 모든 CPU가 같은 버스를 사용하기 때문에 버스 충돌이 있고, 이는 코어 수에 비례한다. 한 CPU가 데이터를 읽는 동안 모든 CPU가 기다리므로 레이턴시가 너무 높다는 문제가 있다.
분산된 메모리 (None Uniform Memory Access)
여러 코어들이 별도의 메모리를 갖고 이를 동기화 하는 방식
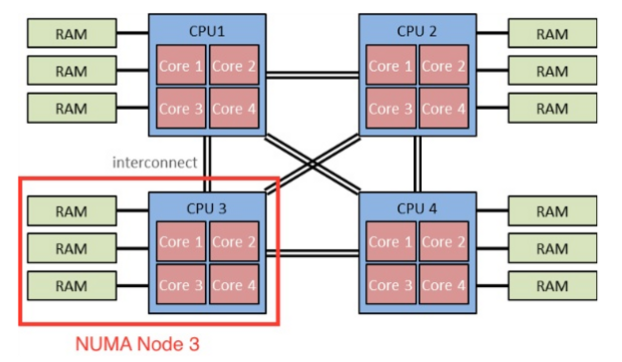
각자 자신의 CPU에 부착된 메모리에 접근하므로 당연히 레이턴시는 짧아진다. 하지만 내 메모리의 데이터가 다른 CPU의 데이터와 같은지 장담할 수 없으므로 계속 동기화를 시도해야하므로 동기화 레이턴시가 존재한다.
암달의 법칙
$$ S = \frac{1}{(1-f) + \frac{f}{n}} $$
$S$는 성능이 향상된 수치, $ f $는 어떤 작업의 병렬화 비율, $ n $은 코어 수를 의미한다.
어떤 작업 ($1$)을 처리하기 위해선 순차적으로 처리하는 부분($(1-f)$)과 병렬적으로 처리하는 부분($\frac{f}{n}$)이 존재한다. 다시 말해 순차적으로 처리한다면 1개의 코어가 담당하므로, 전체에서 $f$만큼을 제외한 부분을 처리하게 되고, 병렬적으로 처리한다면 모든 코어($n$)가 전체에서 $f$만큼을 처리하게 된다. 순차적으로 처리했을 때는 $\frac{1}{1}$이므로 1배만큼 성능을 내게 되지만, 병렬적으로 처리하는 비율을 높이면 분모가 작아지기 때문에 순차적으로 처리할때보다 성능이 몇배만큼 커지는지 알 수 있다.
함정
하지만, 이 그래프를 직접 그려보면 성능 향상이 한계에 부딪힘을 알게 된다.
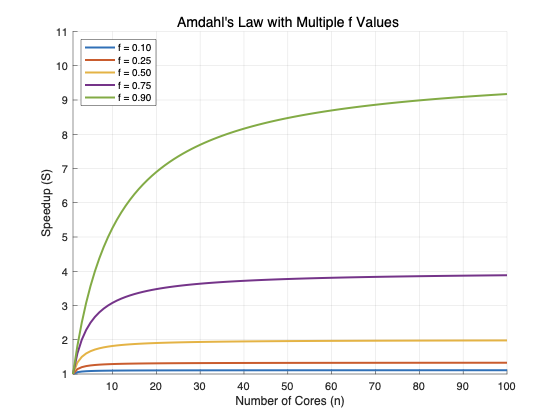
병렬화 비율을 고정하고 코어 수를 점점 늘려보면 위와 같이 어느 임계선을 넘지 못한다는 것을 확인할 수 있다. 코어가 아무리 많아도, 결과적으로는 순차적 처리를 하는 부분$(1-f)$때문에 성능 향상에 제한이 걸리는 것이다.
이 그래프만 보면 멀티코어도 결국 성능 향상에 한계가 있다고 생각할 수 있다.
구스타프슨의 법칙
우선 암달의 법칙은 어떤 작업($1$)을 얼마나 빠르게 처리하는가에 대한 비율을 계산하는 식이다. 즉 작업의 속도를 측정하는 것이라고 볼 수 있다. 병렬화 비율을 많이 높이고, 코어 수를 늘리면 결과값이 높게 나오므로 작업을 엄청 빨리 처리하게 된다고 알 수 있는 것이다.
구스타프슨은 암달의 법칙을 다르게 해석했다. 작업을 얼마나 빠르게 처리하는가가 아니라, 정해진 시간동안 얼마나 많은 작업을 처리하는가에 집중했다.
$$ S(P) = P - \alpha \cdot (P-1) $$
$P$는 프로세서의 수(코어 수), $\alpha$는 순차 처리의 비율, $S$는 성능 향상 수치이다. 정리된 식이므로 원래 식은 다음과 같다.
$$ S(P) = \alpha + P \cdot(1 - \alpha) $$
암달의 법칙과 구스타프슨의 법칙은 서로 성능 향상의 기준을 다르게 보았다.
| 법칙 | 성능 향상의 기준 |
|---|---|
| 암달의 법칙 | 단위 크기 작업의 처리 시간 비율 |
| 구스타프슨의 법칙 | 단위 시간동안 처리하는 작업의 양 |
이를 통해 암달의 법칙을 해석하는 연구자들은 성능 향상이 한계에 부딪쳤음이 아니라, 관점을 다르게 본다면 성능 향상이 가능하다는 것을 알게 되었다고 한다.
'대학교 공부 > 멀티코어프로그래밍' 카테고리의 다른 글
| 멀티코어프로그래밍 (5) - OpenCL 프로젝트 최적화 (0) | 2025.06.14 |
|---|---|
| 멀티코어프로그래밍 (4) - OpenCL 프로젝트 후기 (0) | 2025.06.14 |
| 멀티코어프로그래밍 (3) - [논문 리뷰] Extending Amdahl’s Law for Energy-Efficient Computing in the Many-Core Era (0) | 2025.06.14 |
| 멀티코어프로그래밍 (2) - Cache coherence (0) | 2025.06.14 |
댓글